Learning-Based Joint Super-Resolution and Deblocking for a Highly Compressed Image
Li-Wei Kang, Member, IEEE, Chih-Chung Hsu, Student Member, IEEE, Boqi Zhuang, Chia-Wen Lin, Senior Member, IEEE, and Chia-Hung Yeh, Senior Member, IEEE
Department of Electrical Engineering
National Tsing Hua University
Hsinchu 30013, Taiwan
Abstract
| A highly
compressed image is usually not only of low-resolution, but also
suffers from compression artifacts (blocking artifact is treated as
an example in this paper). Directly performing image
super-resolution (SR) to a highly compressed image would also
simultaneously magnify the blocking artifacts, resulting in
unpleasing visual experience. In this paper, we propose a novel
learning-based framework to achieve joint single-image SR and
deblocking for a highly-compressed image. We argue that individually
performing deblocking and SR (i.e., deblocking followed by SR, or SR
followed by deblocking) on a highly compressed image usually cannot
achieve a satisfactory visual quality. In our method, we propose to
learn image sparse representations for modeling the relationship
between low and high-resolution image patches in terms of the
learned dictionaries for image patches with and without blocking
artifacts, respectively. As a result, image SR and deblocking can be
simultaneously achieved via sparse representation and MCA
(morphological component analysis)-based image decomposition.
Experimental results demonstrate the efficacy of the proposed
algorithm. Keywords: image super-resolution, sparse representation, dictionary learning, self-learning, image decomposition, morphological component analysis (MCA). |
Quick Menu
Data
Matlab source code (32-bit Matlab only)

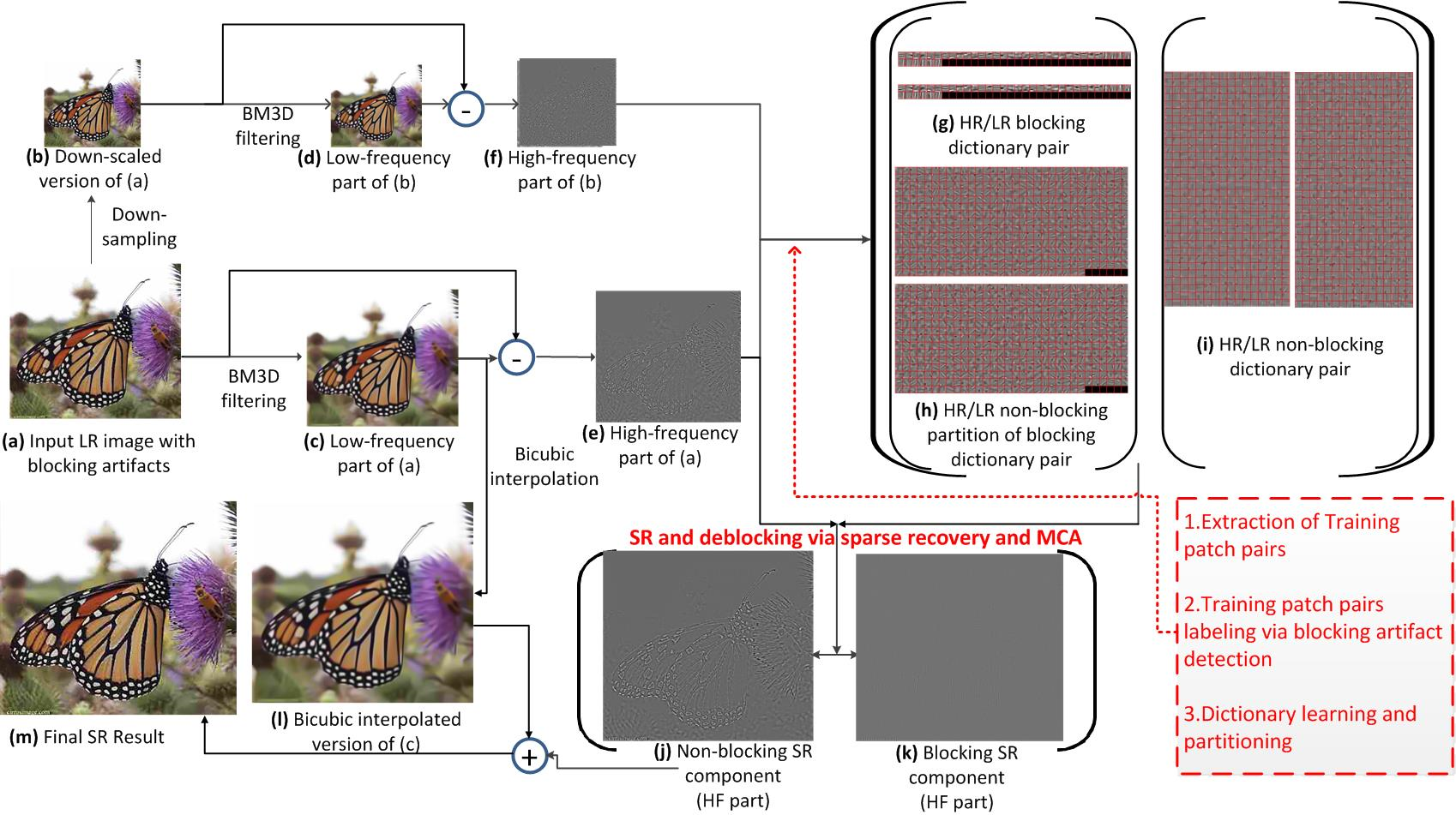
Figure 1. Flowchart of the proposed self-learning-based super-resolution framework for a highly compressed image.
Figure 1 depicts the proposed framework for
self-learning-based joint SR and deblocking for enhancing a downscaled and
highly compressed image. Our method is to formulate the image enhancement
problem as an MCA-based image decomposition problem via sparse representation.
In our method, an input LR image I [see Fig. 1(a)] with blocking artifacts and
its down-scaled version 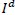 [see Fig. 1(b)] are first
roughly decomposed into the corresponding low-frequency (LF) parts,
[see Fig. 1(b)] are first
roughly decomposed into the corresponding low-frequency (LF) parts,
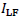 and
and 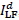 , and the
high-frequency (HF) parts,
, and the
high-frequency (HF) parts, 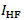 and
and
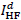 , respectively. Then, the respective most basic
information will be retained in the LF parts [see Figs. 1(c) and 1(d)] while the
blocking artifacts and the other edge/texture details will be included in the HF
parts [see Figs. 1(e) and 1(f)] of the images. Then, we classify all of the
patches in
, respectively. Then, the respective most basic
information will be retained in the LF parts [see Figs. 1(c) and 1(d)] while the
blocking artifacts and the other edge/texture details will be included in the HF
parts [see Figs. 1(e) and 1(f)] of the images. Then, we classify all of the
patches in 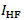 together with their corresponding
patches in
together with their corresponding
patches in 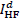 into two clusters of “blocking” and
“non-blocking” HR/LR patch pairs. Based on the two training sets of patch pairs
extracted from the input image itself, we learn two sets of coupled
dictionaries,
into two clusters of “blocking” and
“non-blocking” HR/LR patch pairs. Based on the two training sets of patch pairs
extracted from the input image itself, we learn two sets of coupled
dictionaries, 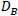 and
and 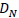 ,
used for SR of blocking and non-blocking patches, respectively, as illustrated
in Figs. 1(g) and 1(h), and Fig. 1(i).
,
used for SR of blocking and non-blocking patches, respectively, as illustrated
in Figs. 1(g) and 1(h), and Fig. 1(i).
To achieve the SR of 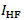 , we
perform patch-wise sparse reconstruction with the coupled dictionary set
, we
perform patch-wise sparse reconstruction with the coupled dictionary set
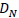 [see Fig. 1(i)] for each patch without blocking
artifacts in
[see Fig. 1(i)] for each patch without blocking
artifacts in 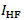 . For each patch with blocking
artifacts in
. For each patch with blocking
artifacts in 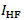 , we perform SR reconstruction with
, we perform SR reconstruction with
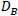 , consisting of
, consisting of 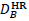 and
and
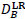 , of corresponding HR/LR atoms, respectively, and
MCA-based image decomposition to obtain the underlying HR patch. Then,
, of corresponding HR/LR atoms, respectively, and
MCA-based image decomposition to obtain the underlying HR patch. Then,
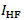 can be simultaneously enlarged and decomposed into
HR non-blocking and HR blocking components [see Figs. 1(j) and 1(k)]. We then
add
can be simultaneously enlarged and decomposed into
HR non-blocking and HR blocking components [see Figs. 1(j) and 1(k)]. We then
add 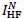 to the bicubic-interpolated
to the bicubic-interpolated
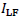 [see Fig. 1(l)] to obtain the final SR result of
I, as illustrated in Fig. 1(m). The detailed method will be elaborated below.
[see Fig. 1(l)] to obtain the final SR result of
I, as illustrated in Fig. 1(m). The detailed method will be elaborated below.
Several LR JPEG images and YouTube videos with blocking artifacts were used to evaluate the performance of the proposed method. In our experiments, all of the test LR images were compressed by JPEG with quality factor (QF) ranging from 15 to 25. Different from [4], where the JPEG compression QF is required to be known in advance, our approach does not require any prior knowledge (including QF) about an input LR image. The parameter settings of the proposed method are described as follows. For each test LR image of size ranging from 140×140 to 442×400, the magnification factor, HR/LR patch sizes, the number of training iterations for dictionary learning, and the size (number of atoms) of each learned dictionary (including
|
Q factor: 15 Choose one method you want to see by clicking follows buttons. |
 |
| Choose one image you want to see by clicking follows image. |
|
|
Click here to download all results without local zoom-in. |
To obtain the best quality of the demo videos, we suggest that the resolution of YouTube player could be adjusted as higher as it can. In these four videos, they are downloaded directly from YouTube with their naive resolution. In this case, there is no ground truth as reference.
|
Description:
|
|
Description:
|
|
Description:
|
|
Description:
|